En este trabajo se hace un análisis estadístico de la organización del drenaje en una cuenca de alta montaña: el tramo superior del arroyo Las Lajas, departamento Río Cuarto, Córdoba (Fig. 1). El arroyo Las Lajas nace en las sierras de Comechingones y confluye con el arroyo Santa Catalina luego de un recorrido de aproximadamente 100 km. La cuenca alta del arroyo Las Lajas está comprendida entre cotas de 750 m y 1200 m s.n.m., topográficamente por encima del quiebre de pendiente que la separa de la cuenca media. La cuenca alta cubre un área de 41 km2 en el ámbito de la provincia geológica de Sierras Pampeanas,
sobre un sustrato de un basamento plutónico-metamórfico del Precámbrico-Paleozoico inferior. El relieve actual de las sierras de Comechingones se desarrolló durante los movimientos ándicos en el Cretácico-Terciario, a partir de una amplia superficie de erosión de la que hoy sólo quedan algunos relictos en sectores cumbrales. El ambiente serrano está conformado por una alternancia de valles poco profundos, de fondo plano, con un importante relleno aluvial y coluvial, presumiblemente de edad holocena. La precipitación media anual en esta área es de 860 mm, con régimen torrencial en los meses de verano.
sobre un sustrato de un basamento plutónico-metamórfico del Precámbrico-Paleozoico inferior. El relieve actual de las sierras de Comechingones se desarrolló durante los movimientos ándicos en el Cretácico-Terciario, a partir de una amplia superficie de erosión de la que hoy sólo quedan algunos relictos en sectores cumbrales. El ambiente serrano está conformado por una alternancia de valles poco profundos, de fondo plano, con un importante relleno aluvial y coluvial, presumiblemente de edad holocena. La precipitación media anual en esta área es de 860 mm, con régimen torrencial en los meses de verano.
Figura 1: Mapa de ubicación de la cuenca alta del arroyo Las Lajas.


La cuenca alta del arroyo Las Lajas está estructuralmente controlada por la Falla Las Lajas, una falla inversa de alto ángulo de rumbo N30ºE, cuya traza aproximadamente coincide con el eje de la cuenca. Esta falla fue reactivada durante los movimientos terciarios y tiene evidencias de actividad neotectónica (Sagripanti 1999; comun. pers. 2002). La litología del sustrato es contrastante a un lado y otro de la Falla Las Lajas; al oeste dominan afloramientos de granitoides y al este de metamorfitas y mármoles, con asomos menores de ortogneises (Otamendi 1998). Varias fallas menores se agrupan en dos conjuntos principales de rumbo NNO y NNE (Fig. 2).
Figura 2: Mapa geológico de la cuenca alta del arroyo Las Lajas.


El análisis morfométrico de cuencas de drenaje ha recibido escasa atención en la Argentina, a juzgar por la aparente escasez de trabajos publicados sobre ese tema (e.g. Guido y Busnelli 1996). En este contexto la presente contribución da una base sólida para la discusión de la morfometría de cuencas de drenaje en la Argentina.
El presente estudio tiene dos propósitos. Uno es caracterizar la cuenca alta del arroyo Las Lajas en base a varias de sus carácterísticas morfológicas y determinar si la conspicua segmentación estructural y litológica en el sustrato de la cuenca se refleja en la organización de la red de drenaje. El otro es explorar el significado estadístico de varios índices morfométricos de uso común.
Metodología y definiciones
La morfometría pretende hallar parámetros que sirvan para caracterizar un ambiente geomorfológico y que, además, sean susceptibles de un tratamiento estadístico o matemático que permita disminuir la influencia de la subjetividad en las conclusiones que se deriven de esos parámetros. En particular, la morfometría de cuencas de drenaje ha reunido un conjunto numeroso de parámetros que representan propiedades inherentes al sistema fluvial. Horton (1945), Schumm (1956) y Strahler (1957) fueron pioneros en la caracterización morfológica cuantitativa de cuencas de drenaje.
Strahler (1957) propuso una clasificación de cursos fluviales basada en la organización de los tributarios, de modo que un curso de orden 1 carece de tributarios, uno de orden 2 es formado por la confluencia de dos cursos de orden 1, uno de orden 3 es formado por la confluencia de dos de orden 2, y así siguiendo. Como corolario el orden de una cuenca de drenaje está dado por el curso de orden mayor. En este esquema la cuenca alta del arroyo Las Lajas es de orden 6. Para el análisis de la organización del drenaje en esta cuenca se delinearon las subcuencas de orden 3, obteniéndose 51 subcuencas, distribuidas 24 en el sector sudoccidental (subcuencas 1 a 14) y 27 en el nororiental (subcuencas 25 a 51) (Fig. 3). De cada subcuenca se midió el área, la cota topográfica máxima en la divisoria de aguas (Alt Máx), la cota topográfica en la desembocadura a la cuenca media (Alt Mín), la longitud entre la desembocadura y la divisoria de aguas en dirección aproximadamente paralela al curso de orden 3 (Long.) y por último, se calculó la sumatoria de las longitudes y el número de los cursos de orden 1 y separadamente, de órdenes 2 y 3 (Cuadro 8 ; las longitudes están expresadas en km y las áreas en km2).
Figura 3: Red de drenaje y subcuencas de orden 3, en la cuenca alta del arroyo Las Lajas. Las subcuencas están numeradas correlativamente en el sentido de las agujas del reloj.


Estos datos fundamentales para el cómputo de los parámetros morfométricos fueron obtenidos de las siguientes fuentes.
· La divisoria de cuenca principal fue digitalizada de las cartas topográficas del IGM, La Punilla, Hoja 3366-23-2 y La Barranquita, Hoja 3366-24-1, con una equidistancia de 50 m.
· La red de drenaje se digitalizó de un mapa a escala 1:20.000 basado en fotografías aéreas.
· Las divisorias de las subcuencas fueron dibujadas sobre el mapa de la red de drenaje empleando las hojas topográficas del IGM.
· La planimetría se basó en una imagen LANDSAT TM georeferenciada.
En el análisis de la cuenca alta del arroyo Las Lajas se emplearon varios parámetros morfométricos cuya constitución está dada en el cuadro 1 y cuyo significado se describe a continuación. La densidad de drenaje (Dd) es una expresión de la textura fluvial, o grado de disección de una cuenca. De modo general, Dd está gobernada por el tipo de precipitación, la densidad de la cubierta vegetal, la topografía y el tipo de suelo, entre otros factores. El valor de Dd puede variar de menos de 10 en áreas con predominio del escurrimiento subterráneo sobre el superficial, e.g. terrenos kársticos o de arena suelta y densa cubierta vegetal, a más de 100 en terrenos arcillosos impermeables (badlands) sin vegetación (Chorley et al. 1984). La frecuencia de cursos de primer orden (F1) caracteriza la capacidad de expansión de la red de drenaje y permite realizar inferencias acerca del estado de equilibrio de la red. La rugosidad de cuenca (Rd) vincula la densidad de drenaje con el relieve. Cuencas muy disectadas con bajo relieve presentan un índice de rugosidad similar a cuencas moderadamente disectadas y con alto relieve (Patton 1988).
La relación de bifurcación (Rb) describe un aspecto de la organización de la red. La relación de bifurcación media para cada subcuenca se obtuvo como promedio de las relaciones parciales: (Rb12 + Rb23)/2. En el esquema de Strahler (1957), el menor valor teórico de Rb es 2, y corresponde a dos tributarios y un colector. Una red de drenaje de tipo dendrítico tiende a valores altos de Rb, mientras que una de tipo paralelo, con fuerte control estructural, puede dar valores próximos a 2. Los números de cursos de cada orden están relacionados por un factor geométrico y caen sobre una línea recta si se grafican respecto del orden en papel semilogarítmico. Esta relación se conoce como la ley de Horton de número de cursos.
La relación de longitudes medias (Rl) por subcuenca se obtuvo como promedio de los valores parciales. La relación de elongación (Relong) es un parámetro de forma de la cuenca. Las sumatorias de las longitudes de los cursos para cada orden están relacionados geométricamente y caen sobre una línea recta si se grafican en papel semilogarítmico. Esta relación se conoce como ley de Horton de longitud de cursos.
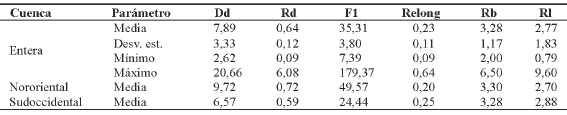
Los valores de los parámetros morfométricos calculados para la cuenca alta del arroyo Las Lajas están tabulados en el cuadro 9 y sus estadísticos fundamentales se dan en el cuadro 2.
Cuadro 2: Estadística de los parámetros morfométricos empleados; valores sin transformar.

Análisis estadístico y resultados
La figura 4 muestra la relación semilogarítmica que existe entre el número de cursos de cada orden y la longitud total de cursos de cada orden respecto del orden de drenaje. La relación entre números de cursos es lineal y se ajusta bien a la ley de Horton de números de cursos, que predice una relación geométrica con factor aproximadamente igual a 3. La relación entre longitudes de cursos muestra un desvío que probablemente refleja una excesiva longitud de cursos de orden 3.
Figura 4: Gráfico de Rl (Serie1) y de Rb (Serie 2) versus el orden de Strahler.


Prueba de normalidad y correlación
El primer paso en el análisis estadístico fue determinar si los parámetros morfométricos se adecuan a distribuciones normales y en caso contrario, si pueden transformarse para que lo hagan. Se empleó la prueba no paramétrica de Kolmogorov (Gibbons et al. 1992) que consiste en determinar D, (estadístico de la prueba) que da la separación mayor en porcentaje entre la curva acumulativa normal y la distribución empírica. En su forma original casi ninguno de los parámetros se ajusta a una distribución normal. En consecuencia, fueron transformados a lognormales (logaritmo neperiano) y normalizados y estandarizados (restados de la media y divididos por la desviación estándar). La estandarización hace que cada parámetro contribuya igualmente a la varianza total. Transformados de esta manera todos los parámetros se ajustan a una distribución normal, a juzgar por los resultados de una prueba de Kolmogorov (Cuadro 3). Así, pues, es aceptable proseguir con el tratamiento estadístico empleando métodos paramétricos, generalmente más poderosos que los no paramétricos.
Cuadro 3: Prueba de Kolmogorov de ajuste a una distribución normal.


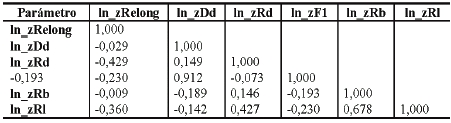
En el Cuadro 4 se dan los coeficientes de correlación de Pearson (Cox et al. 1974) para los parámetros morfométricos seleccionados, en su transformación lognormal y estandarizados. En general, la correlación entre pares de parámetros da valores bajos, lo cual sugiere que existe una débil interacción entre parámetros. La principal excepción se da entre F1 y Dd con un r = 0,912. Una alta correlación positiva entre estos dos parámetros es de esperar, sin embargo, ya que ambos miden, de modo diferente, la densidad del drenaje superficial. Se aprecia, además, una correlación positiva moderada entre Rb y Rl que puede deberse a que la longitud de los cursos entra en el cómputo de Rb. Se optó por retener estos parámetros a pesar de su interacción por dos razones: éste es un estudio exploratorio y los parámetros seleccionados son de amplio uso en morfometría.
Cuadro 4: Matriz de correlación.

Comparación de muestras
La diferente litología a uno y otro lado de la Falla Las Lajas podría estar reflejada en los valores de los parámetros morfométricos. Para comprobar esta hipótesis se compararon las subcuencas de tercer orden a un lado y otro de la falla (Fig. 3). La prueba estadística consistió en determinar si existen diferencias significativas en los valores medios de los parámetros para cada grupo de subcuencas.
Se llevó a cabo una prueba de t (Student) para dos muestras independientes para cada par de parámetros. Previamente, la prueba de Levene (Montgomery 2000) para igualdad de varianzas demostró que Dd y F1 difieren significativamente en cada grupo (Cuadro 5, columnas 6 y 7, valores del estadístico de Fisher, F, elevados, y un significado inferior a alfa = 0,05); para estos dos parámetros, t se calculó suponiendo varianzas disímiles. La prueba de Student indica medias significativamente diferentes sólo para Dd y F1 (Cuadro 5, columnas 8 a 10); las medias de los demás parámetros no permiten discriminar entre subcuencas del sector oriental y del occidental.
Cuadro 5: Prueba de Student para subcuencas orientales y occidentales.
Análisis de agrupamiento
Dado que la separación de las subcuencas en un grupo oriental y otro occidental, a primera vista atractiva, no parece ser natural, se exploró la posibilidad de que exista otro agrupamiento natural. Para ello se empleó el análisis de agrupamiento (cluster analysis) basado en una matriz de distancias euclidianas elevadas al cuadrado y el método de enlace de Ward. El resultado de este análisis está resumido en el dendrograma de la figura 5. El dendrograma sugiere una tendencia a la formación de tres a cuatro grupos a una distancia estadística de alrededor de 5 pero la reiteración de cálculos variando el método de enlace (e.g. simple, promedio) muestra que una división en más de dos grupos no es estable. Esta técnica dio por resultado un agrupamiento fuerte en dos conjuntos a una distancia estadística de alrededor de 19, uno formado por las 24 subcuencas 1, 4, 10, 11, 13, 21, 22, 26, 28, 29, 31, 32, 33, 35, 36, 37, 38, 39, 40, 46, 47, 49, 50 y 51, y el otro por las 27 restantes. El 72% de las subcuencas del primer grupo corresponden al sector sudoccidental y el 63% de las del segundo grupo corresponden al sector nororiental.
Figura 5: Dendrograma del análisis de agrupamiento jerárquico. Los números a la izquierda corresponden a la numeración de las subcuencas de tercer orden. En el dendrograma, el límite entre los dos grupos más estables pasa entre las subcuencas 3 y 37.


Análisis factorial
El último paso en el análisis de los parámetros morfométricos del arroyo Las Lajas consistió en explorar la estructura de las variables mediante la técnica de análisis factorial (Krumbein y Graybill 196; Rock 1988). Esta técnica sirve para hallar aquellas combinaciones de parámetros que mejor expliquen la varianza total del sistema. El procedimiento consistió, primero, en obtener los valores eigen de la matriz de correlación por el método de Componentes Principales. Los valores eigen representan la varianza del sistema; su suma es igual a la suma de las varianzas de las variables, la cual por efecto de la estandarización es igual al número de variables, o parámetros, en nuestro caso igual a 6. El segundo paso consistió en retener sólo aquellos valores eigen que estén por encima de 1,00, con la premisa de que si un valor eigen vale menos de 1,00 es menos significativo que el parámetro original y, por lo tanto, conviene despreciarlo. Merced a esta selección se retuvieron tres valores eigen. Por último, se rotaron los ejes de coordenadas por el método Varimax, manteniendo la ortogonalidad, es decir, la independencia de los factores. La rotación de ejes busca maximizar la distribución de la varianza en cada factor. Así se obtuvieron los valores eigen que figuran en la columna "Total" del cuadro 6. Cada valor eigen explica una fracción de la varianza del conjunto de parámetros (columna "% de Varianza" del cuadro 6); el valor de esta fracción se obtiene dividiendo el valor eigen por la varianza total, i.e. 6. El valor acumulativo (columna "Acumulativa %" del cuadro 6) indica que los tres componentes retenidos dan cuenta de casi el 86% de la varianza total.
Cuadro 6: Varianza explicada.


Finalmente, el cuadro 7 muestra la correlación entre los parámetros y los tres factores retenidos. Los valores en las celdas son los pesos (loadings) de los componentes. Se aprecia que el factor 1 tiene una alta correlación con Dd y F1, el factor 2 con Rb y Rl, y el factor 3 con Relong y Rd.
Cuadro 7: Matriz de tres componentes rotados según método Varimax.


Interpretación
El análisis de agrupamiento y la comparación de medias indica que existe una tendencia de las cuencas de orden 3 a agruparse en dos conjuntos cuya clasificación respecto de las litologías dominantes es acertada entre el 63 y el 72% de los casos. El tercio restante está mal clasificado, lo cual significa que la agrupación no está enteramente controlada por la Falla Las Lajas y la litología del sustrato.
El análisis factorial indica que tres factores explican casi el 86% de la varianza del sistema. Cada factor está asociado a un par de variables. El factor 1, asociado a Dd y F1, combina longitud y número de cursos y daría cuenta del grado de disección de la superficie de la cuenca. El factor 2, asociado a Rb y Rl, combina los dos parámetros que describen la organización de la red de drenaje. El factor 3 es más difícil de interpretar, ya que está asociado a un parámetro de forma, Relong, con un peso negativo y otro de disección o rugosidad de la cuenca, Rd. La asociación sugiere que cuanto más elongada sea una cuenca mayor será la tendencia a que tenga una alta rugosidad, lo cual podría estar reflejando un control estructural dado por las fallas menores. El análisis de esta posibilidad no pudo llevarse adelante debido a la falta de un mapa estructural definitivo para el área.
Cuadro 8: Mediciones fundamentales en subcuencas de orden 3 de la cuenca alta del arroyo Las Lajas.


Cuadro 9: Parámetros morfométricos computados para la cuenca alta del arroyo Las Lajas.


Conclusiones
Una conclusión de este estudio es que existen evidencias fuertes para suponer que la litología ejerció una influencia importante en la estructuración de la red de drenaje de tercer orden. El sector nororiental, dominado por rocas carbonáticas, se caracteriza por valores más elevados en la densidad de drenaje y número de cursos de primer orden (Cuadro 2).
La diversidad de parámetros morfométricos es grande. Existe por lo menos media docena de parámetros de forma. Cuál emplear, es una pregunta que seguramente no tiene respuesta única. Una ventaja de los parámetros morfométricos es que pueden ser procesados estadísticamente. Sin embargo, muchos de ellos relacionan mediciones fundamentales similares, como por ejemplo el área, lo cual hace que queden más o menos correlacionados entre sí. El análisis estadístico debiera ser precedido por una inspección de la constitución de los parámetros a emplear para detectar aquellos más fuertemente interrelacionados y evitar que oscurezcan otras relaciones más significativas. El estudio morfométrico de la cuenca alta del arroyo Las Lajas demuestra la validez del enfoque cuantitativo, estadístico, para poner a prueba hipótesis de trabajo; en este caso, el posible control de la litología en el diseño de la red de drenaje. Y muestra también la complejidad del análisis y la necesidad de acumular más información, minuciosamente analizada y evaluada, para avanzar en la caracterización de las cuencas de drenaje del noroeste de la Argentina.
Imprimir artículo
| Tweet |

























0 comentarios:
Publicar un comentario
Gracias por tu Comenterio